Answers To “Is This Picture Level?”

A few weeks ago, I asked a few questions about a picture of me on the Turner River^link. I even offered a reward for the best answers. Here are my answers.

First Question

NO, the picture is not level. The photographers’ usual reference point for getting a picture level is the horizon. One of the rules of composition says that your horizon must be perfectly straight (unless it is so far off that the viewer will know that you did it on purpose).

But what if the horizon is not available, as in this picture? Nasim Mansurov, in his article The Importance of Straightening The Horizon and Aligning Lines, discusses (and shows examples of) several options for getting your picture straight. But he didn’t mention this situation.

Q2: How Do We Straighten It?

First, let me say what won’t work: allegedly horizontal elements on a canoe, like seats and thwarts, even in calm water, can be expected to deviate from horizontal as a matter of routine. This case, as it turns out, is no exception. So what can we use?

When you have a calm body of water, as we do here, and the horizon is not visible, you can still depend on the levelness of the water. As I discussed in Reflections – My Answer To “What’s Wrong With This Picture (Version 2)?”, the angle of incidence of a reflected light ray equals the angle of reflection, which means, since the surface of the water is a horizontal plane, that the reflected object will be directly under the object itself, or the line between the two will be vertical, or 90° from the horizon.

Examples

In the picture above, I have identified four different reference lines. Once you are convinced that this works, you only need one. Two things make this more challenging, however. There are floating obstacles obscuring good reflection candidates. Also, as I discussed in “Reflections…”, the reflection won’t look exactly like the reflected object due to the changed perspective. Since identifying the exact point reflected may be subject to slight errors in estimated position, the further they are apart (meaning the longer the line connecting them), the better. That’s because the error in the rotation angle for the picture to be level is proportional to the positional error divided by the distance apart (for small error angles).

In the above picture, the flower (labeled “A”) is an easy choice, but it and its reflection are close together. The hole in the canopy (“B”) and the more prominent branch (“C”), although less identifiable in the reflection, do have good separation distances. “D” shows that in a pinch, when no well-marked points are available, you could even use the point on a curved line where the slope of the curve and the slope of its reflection are the same (or parallel). Expect a higher positional error in cases like that.

Once you have a reference line, most editing software has a horizon-straightening feature, or at least the ability to rotate the image until your reference line is vertical. This image needs to be rotated about 8⅓° clockwise. To see the corrected version, go to the bottom of our Red Mangrove Maze image page (where you can also find the identity of the person who took this picture).

Bonus Question

For the last question of the article, which was a math problem to find my age, see the note below.

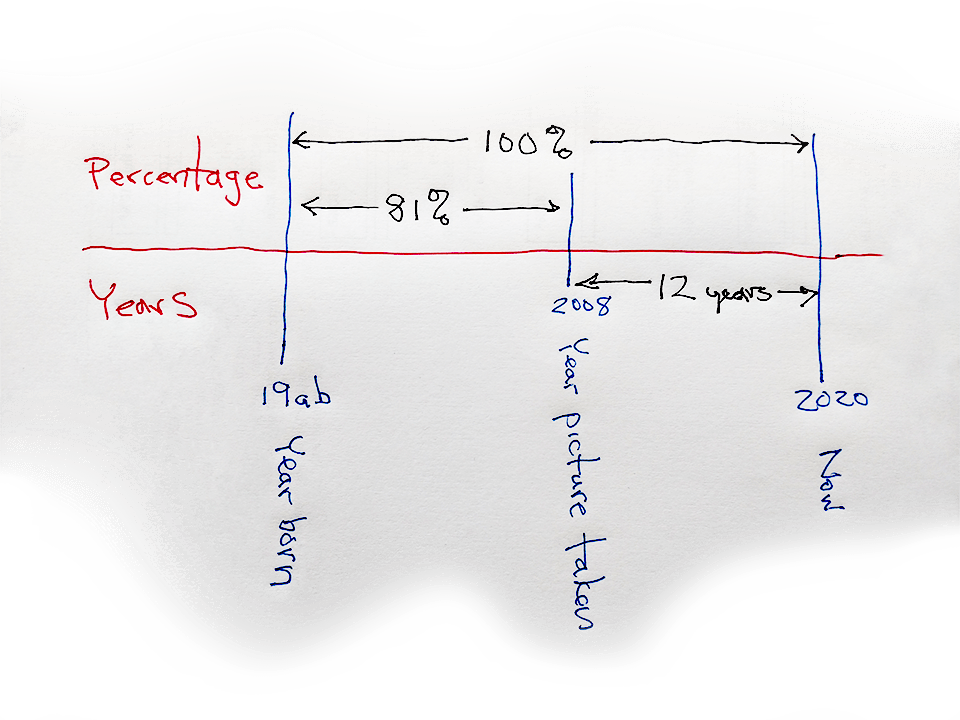
As you can see in the above illustration, there are three related timespans (years before 2008, years after 2008, and total years); if you know any two, you can find the third. That is true whether you are talking in years or percentages. We want the answer in years, but we only know one of the three. We know two of the three as a percentage, so we can (and will) know all three. What we have to do, then, is find the relationship between years and percentages.

Twelve years is less than 19% of my current age,

or \( 12 \leq 0.19 \times Age \)

\( Age \geq \frac{12}{0.19} \approx 63.2 \)

Actually, I’m about 64½.

Your reward (including bonus) would be \( \frac{1}{0.81} \approx 1.23 \) times the original award, meaning your bonus would be about 23%.

And The Winner Is…

There were four responses to the original post. All addressed the title question. Nobody addressed the follow-up or bonus questions. The judges have concluded that the first correct answer and winner of this contest, receiving ten dollars off of any Bee Happy Graphic product or service, and all bragging rights, is M. Alexander (former member of Kendall Camera Club). Congratulations!