Non-rectangular Tray Mat Math

Warning: if you don't enjoy math, you may not enjoy this article!

We are here to determine the angle between a cove mat wall's base and its edge. These angles are labeled with α (the Greek letter alpha) in Figure C1 below.

Illustration of our example cove mat — Figure C1

Although we used three-dimensional vector math in a simpler case of this problem (Link), here we stick with a two-dimensional approach. In Figure C1, we've drawn the dashed purple lines to represent the horizontal (relative to the base line of the right wall) and its perpendicular component of the right triangle needed to solve for α_R.

Key to solving this problem are the yellow and the orange right triangles. The long "opposite" side of the orange triangle is S_R. Therefore the tan(φ) = S_R / short "adjacent" side, meaning that short side = S_R / tan(φ).

On the yellow triangle, the sin(φ) = S_L / hypotenuse, meaning that the hypotenuse = S_L / sin(φ).

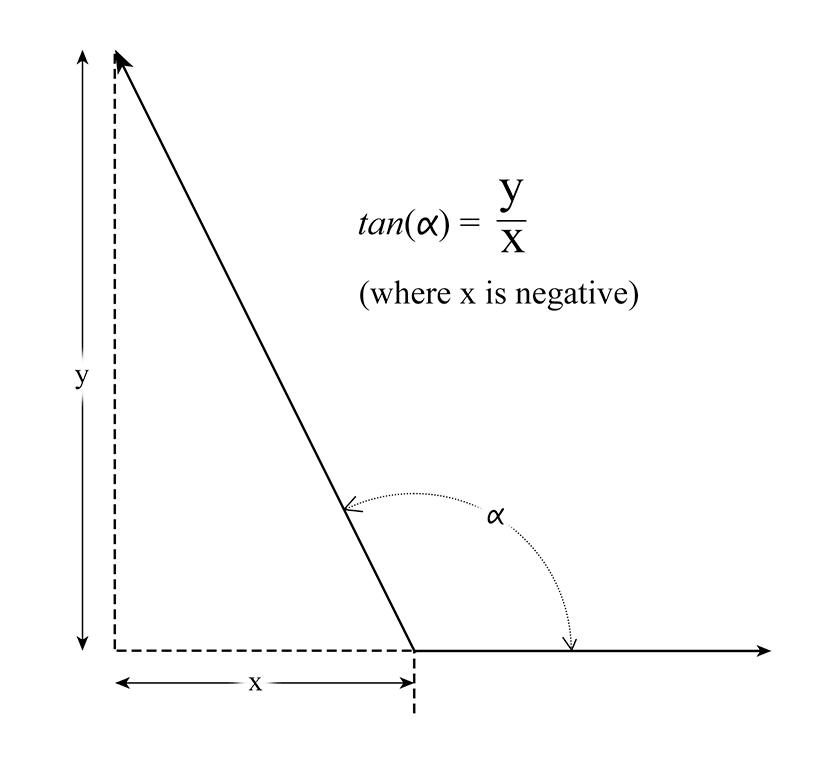
Illustration of the definition of the tangent for an obtuse angle — Figure C2: Illustration of the tangent of an obtuse angle

Comparing Figure C2 to Figure C1, the purple dashed line running along the right side of the orange triangle represents y in Figure C2. It is the same as W_R. The purple-dashed segment along the tope edge of Side R represents x, and can be seen to equal

$\frac{S_{R}}{\tan (φ)} + \frac{S_{L}}{\sin (φ)}$

Therefore,

$\tan (α_{R}) = \frac{W_{R}}{- (\frac{S_{R}}{\tan (φ)} + \frac{S_{L}}{\sin (φ)})}$

This is how we got the results in the "Finding Alpha" section of "Making Tray Mats With Non-rectangular Bases". Any questions?