Cove Mat Math

Warning: if you don't enjoy math, you may not enjoy this article.  Do not panic!

We are here to determine the angle between a cove mat wall's base and its edge. These angles are labeled with α (the Greek letter alpha) in the "Back of Mat" view in Figure 1 and in Figure B1 below. This can be solved with a bit of three-dimensional vector math, which you would have probably seen as a junior or senior in high school as either "trigonometry and analytic geometry" or "pre-calculus" (a title I don't like because although it sounds more impressive, it is less descriptive and could theoretically include your fourth-grade multiplication tables).

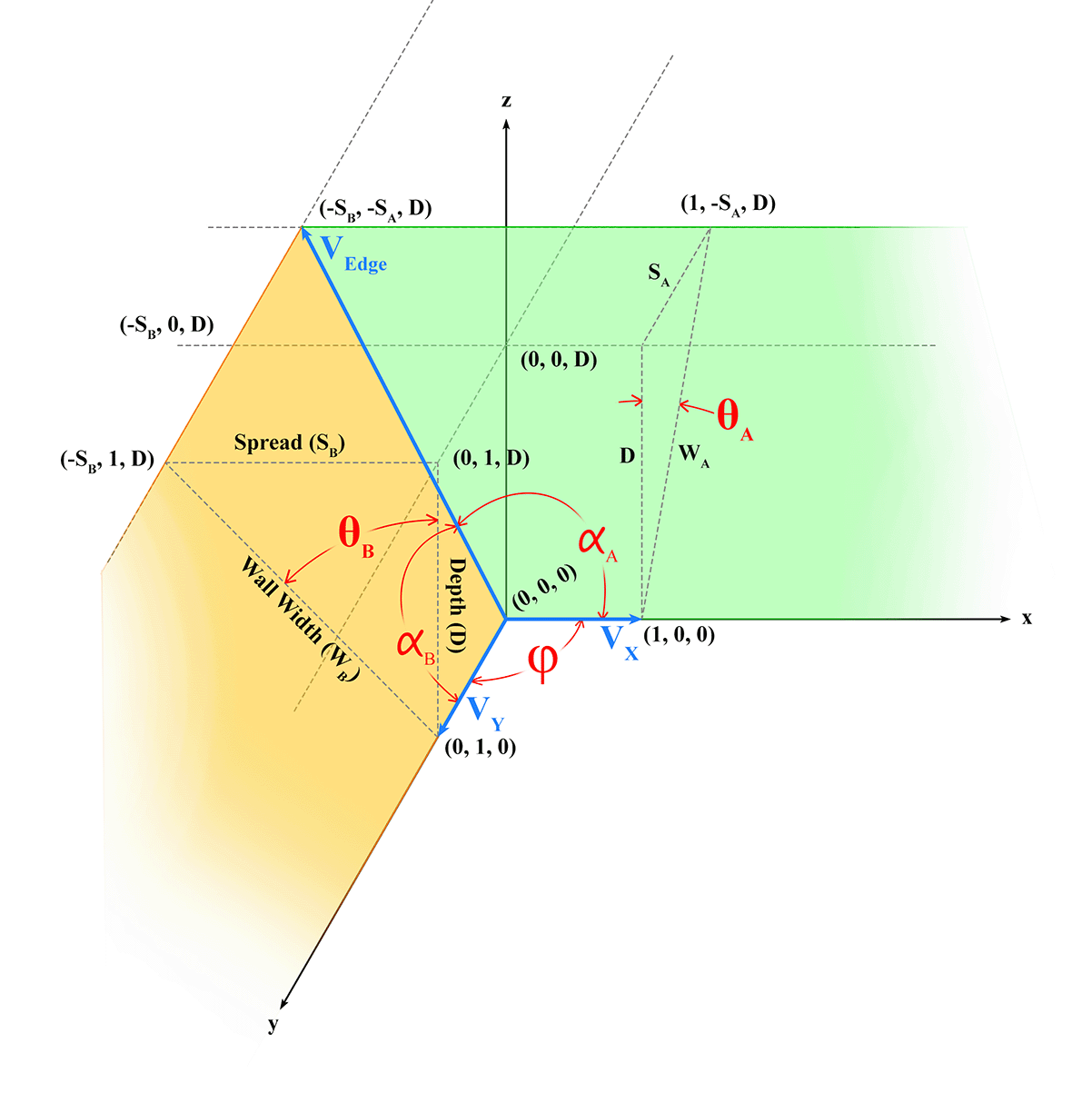
In the above figure, we've aligned one corner of the base of a cove mat with the origin of the xy axis to make things easier, and where possible we've picked vectors with as many zeros and ones as possible. α could be described as the angle between the vector V_Y, whose x, y, z coordinates are (0, 1, 0) and vector V_Edge with coordinates (-S_B, -S_A, D), showing that it ends at the top corner of the finished cove mat, D (for Depth) units (inches) above the base, and S (for Spread) inches beyond the base's edge along both the x and y axes. For what it's worth, we could have picked any number of parallel vectors for V_Y, but why would we want to?

One way to find the angle between two vectors is to use the relationship:

$$\cos \left(\alpha \right)=\frac{(V_Y,V_{\mathrm{Edge}})}{\left|V_Y\right|\left|V_{\mathrm{Edge}}\right|}$$

That numerator is the dot product of two vectors. In general terms, the dot product of V₁ with coordinates (x₁, y₁, z₁) and V₂ with coordinates (x₂, y₂, z₂) is x₁x₂ + y₁y₂ + z₁z₂. In our case, that would be 0(-S_B) + 1(-S_A) + 0(D) = -S_A (Don't you just love zeros and ones?).

The vertical lines surrounding each vector in the denominator represent the length of that vector. In three dimensions, the Pythagorean theorem turns into

$$\left|V_1\right|=\sqrt{x_1^2+y_1^2+z_1^2}$$

In our case

$$\left|V_Y\right|=\sqrt{0^2+1^2+0^2}=1$$

and

$$\left|V_{\mathrm{Edge}}\right|=\sqrt{{\left({\mathrm{-S}}_B\right)}^2+{\left({\mathrm{-S}}_A\right)}^2+D^2}$$

Hence

$${\alpha }_B={\cos }^{-1}\left(\frac{\mathrm{-}{S}_A}{\sqrt{S_B^2+S_A^2+D^2}}\right)$$

To simplify even more, we will work backwards using the Pythagorean Theorem to create the triangle in Figure B2 to the right to represent α. The vertical opposite side of this triangle would be

$$\sqrt{{\mathrm{Hypotenuse}}^2-{\mathrm{Adjacent}}^2}$$

or

$$\sqrt{(S_A^2+S_B^2+D^2)-S_A^2}=\sqrt{S_B^2+D^2}$$

So a slightly simpler formula would be

$${\alpha }_B={\tan }^{-1}\left(\frac{\mathrm{-}\sqrt{S_B^2+D^2}}{S_A}\right)$$

This is how we got the results in the "Finding Alpha" section of "Making Cove Mats".  This article was made possible by Mr. Titskowski, the finest math teacher at Santiago High School (probably retired). Any questions?